Kamis, 09 Juni 2011
PERBEDAAN THUMBSUCK dan RAMPOK
Thumbsuck dan Rampok > software yang berfungsi untuk mencuri isi flashdisk.
akan meng-copy file yang terdapat pada flashdisk yang dicolokkan
kekomputer tempat Thumbsuck dan Rampok terinstall
1. Dari segi akses cibiliti
Thumbsuck dan Rampok sama_sama dapat dioperasikann dengan mudah oleh pengguna awam.
2. segi Fisibilitas
Rampok.exe tidak muncul dalam task list process di task manager saat dijalankan
sedangkan Thumsuck.exe muncul dalam task list process di task manager saat
dijalankan
3. Kesederhanaan
Rampok menggunakan tombol on/off untuk di aktifkan atau menonaktifkan kerja program sedangkan Thumbsuck tidak.
4. Efisiensi
thumbsuck dan rampok meminimasi pergerakan mata pada saat running karena data dari hasil korban di simpan dalam 1folder.
5. Konsistensi
Thumbsuck dan Rampok digunakan untuk mencuri maka kerja programnya tidak nampak pada layar sesuai dengan pencuri yang ada pada dunia nyata.
6. Prediktabilitas
7. Kontrol dan Fleksibilitas
Thumsuck dan Rampok dapat di atur dimana temapt letak hasil curian sesuai yang
kita inginka dan pengkopian data dari si korban bekerja dengan cepat.
8. Responcibilitas
dalam kasus ini responcibilitas Thumbsuck dan Rampok bekerja begitu sensitif
terhadap flashdisk yang masuk.
9. Penanganan kesalahan
dalam kasus ini thumbsuck dapat running tanpa ada penggunaan password, berbeda dengan Rampok yang memiliki password dan username untuk d running dan apabila kita kelupaan kode sandi dan username, rampok maka kita dapat mengetahuinya dengan cara buka file "mdb" pada c:\windows\system32
10. kejelasan arti dan tujuan setiap komponen pembentuk sistem
11. Kejelelasan antar komponen dan system secara keseluruhan mudah dimengerti
karena cara kerja program thumbsuck dan rampok begitu mudah dipahami karena
bekerja dengan cara mengcopy seluruh file yg ada pada flashdisk
12. Enak Di pandang
Thumbsuck dan rampok memiliki icon yang begitu cantik dan menarik pad file
hasil curian tadi
13. Kesan pertama yang positif
dalam kasus ini,user pasti akan ketagihan menggunakan software ini karena dapat
mencuri data secara diam-diam.
14. strade off
Minggu, 03 April 2011
Tahap Awal Belajar Audio Mixdown Dengan Adobe Audition...
* Lalu muncul tampilan berikut :
* Masukkan musik yang diinginkan dengan menekan Import File dan pilih musik
* Tarik musik yang diimport tadi ke dalam track
* Mengatur volume musik naik turun
* Mengatur Pan Speaker Kiri-Kanan
* memotong-motong musik
* Gabungkan hasil rekaman dengan musik yg anda import tadi sesuai selera
* Setelah semua selesai diedit, maka kita save dengan format .ses
* Klik file, save session
* Lalu kita juga bisa mengexportnya dengan berbagai format yang tersedia
* Klik file, export, audio mixdown
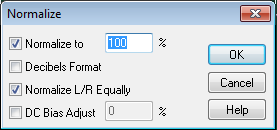
* Setelah export kita Normalize file musik kita
* Ambil Effect, Amplitude, Normalize (process)
* Standarnya 100% lalu OK
* Kemudian agar tidak terjadi distorsi, maka kita buat hard limiting
process-nya jika terjadi ini
* Pilih Effect, Amplitude, Hard Limiting (process)
* Batasi max Amplitudonya. Contoh : -.1
* Lalu OK
* Kemudian save kembali
* Selesai
kesimpulan
1. Dengan ini kita bisa membuat sebuah musik dapat digabungkan dengan musik lain
dan juga dapat diberi effeck
2. File yang bisa diedit kembali adalah file dengan format .ses
Rabu, 04 Agustus 2010
tugas searching and sorting
#include
#include
void main(){
int arr[100],i,element,no;
clrscr();
printf("\nEnter the no of Elements: ");
scanf("%d", &no);
for(i=0;i
scanf("%d",&arr[i]);
}
printf("\nEnter the element to be searched: ");
scanf("%d", &element);
for(i=0;i
printf("\nElement found at position %d",i+1);
getch();
exit(1);
}
}
printf("\nElement not found");
getch();
}
Output:
Enter the no of Elements: 5
Enter Element 1: 12
Enter Element 2: 23
Enter Element 3: 52
Enter Element 4: 23
Enter Element 5: 10
Enter the element to be searched: 23
Element found at position 2
Senin, 05 Juli 2010
Tugas 8
1. Register Buffer Terkendali
Gambar di atas memperlihatkan sebuah register bufer terkendali dengan CLR aktif tinggi. Artinya jika CLR tinggi, semua flip-flop mengalami reset dan data yang tersimpan menjadi Q = 0000. Ketika CLR kembali ke keadaan rendah, register telah siap untuk beroperasi.
LOAD merupakan masukan kendali yang menentukan operasi rangkaian. Jika LOAD rendah, isi register tidak berubah. Jika LOAD tinggi, dengan tibanya tepi positif sinyal detak, bit-bit X dimasukkan dan data yang tersimpan menjadi :
Q3Q2Q1Q0 = X3X2X1X0.
Ketika LOAD kembali ke keadaan rendah, kata tersebut telah tersimpan dengan aman. Artinya, bit X dapat berubah tanpa mengganggu kata yang telah tersimpan tadi.
2. Register Geser Terkendali
sebuah register geser terkendali (controlled shift register) mempunyai masukan-masukan kendali yang mengatur operasi rangkaian pada pulsa pendetak yang berikutnya. Jika SHL rendah maka sinyal SHL tinggi. Keadaan ini membuat setiap keluaran flip-flop masuk kembali ke masukan datanya. Karena itu data tetap tersimpan pada setiap flip-flop pada waktu pulsa-pulsa detak tiba.
Jika SHL tinggi, D in akan masuk ke dalam flip-flop paling kanan, Q 0 masuk ke dalam flip-flop kedua, Q1 masuk ke dalam flip-flop ketiga, dan seterusnya. Dengan demikian rangkaian bertindak sebagai register geser kiri.
Senin, 03 Mei 2010
tugas 5
Buatlah tabel penjumlah A= 5, B=3 dengan prinsip full adder, kemudian buat gambar rangkaian dan jelaskan prinsip kerjanya?
gambar Rangkaian
|
| A | B | Cin | SUM | CARRY |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 |
|
|
|
|
|
|
|
| NB: |
|
|
|
|
|
| A = INPUT 1(5) |
|
|
|
| |
| B = INPUT 2(3) |
|
|
|
| |
| C = CARRY DARI PENAMBAH |
|
|
| ||
| SUM = HASIL JUMLAH A + B |
|
|
| ||
| Carry = carry dari sum |
|
|
| ||
Prinsip kerja:
Penjumahan full adder pada prinsipnyamenggunakan dua buah half addaer dan sebuah gerbang OR. Half adder pertama merupakan penjumlahan A dan B . Selanjutnya nilai SUM dari half adder pertama diproses pada half adder kedua dengan input satu lagi yaitu C. Nilai half adder kedua itulah yang menjadi SUM selanjutnya. Carry pada half adder pertama diproses pada gerbang OR.
Minggu, 18 April 2010
tugas 4
(Note: * = AND, + = OR and ' = NOT)
1. A * 1 = 1
2. A * 0 = 0
3. A + 0 = 0
4. A * A = A
5. A * 1 = 1
2. Give the best definition of a literal?
1. A Boolean variable
2. The complement of a Boolean variable
3. 1 or 2
4. A Boolean variable interpreted literally
5. The actual understanding of a Boolean variable
3. Simplify the Boolean expression (A+B+C)(D+E)' + (A+B+C)(D+E) and choose the best answer.
1. A + B + C
2. D + E
3. A'B'C'
4. D'E'
5. None of the above
4. Which of the following relationships represents the dual of the Boolean property x + x'y = x + y?
1. x'(x + y') = x'y'
2. x(x'y) = xy
3. x*x' + y = xy
4. x'(xy') = x'y'
5. x(x' + y) = xy
5. Given the function F(X,Y,Z) = XZ + Z(X'+ XY), the equivalent most simplified Boolean representation for F is:
1. Z + YZ
2. Z + XYZ
3. XZ
4. X + YZ
5. None of the above
6. Which of the following Boolean functions is algebraically complete?
1. F = xy
2. F = x + y
3. F = x'
4. F = xy + yz
5. F = x + y'
7. Simplification of the Boolean expression (A + B)'(C + D + E)' + (A + B)' yields which of the following results?
1. A + B
2. A'B'
3. C + D + E
4. C'D'E'
5. A'B'C'D'E'
8. Given that F = A'B'+ C'+ D'+ E', which of the following represent the only correct expression for F'?
1. F'= A+B+C+D+E
2. F'= ABCDE
3. F'= AB(C+D+E)
4. F'= AB+C'+D'+E'
5. F'= (A+B)CDE
9. An equivalent representation for the Boolean expression A' + 1 is
1. A
2. A'
3. 1
4. 0
10. Simplification of the Boolean expression AB + ABC + ABCD + ABCDE + ABCDEF yields which of the following results?
1. ABCDEF
2. AB
3. AB + CD + EF
4. A + B + C + D + E + F
5. A + B(C+D(E+F))
| TABEL BANTU | |||||||
| A | B | C | A' | B' | C' | B+C | B.C |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| A.B' | A+B' | A.C | A+C | A'.B | A'+B | (A+B)' | (A.B)' |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| Hukum Komulatif | |||
| A+B | B+A | A.B | B.A |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| Hukum Asosiatif | |||
| (A+B)+C | A+(B+C) | (A.B).C | A.(B.C) |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| Hukum Identity | ||||
| A+A | A | A.A | A.B+A.B' | (A+B).(A+B') |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| Hukum Distributif | |||
| A.(B+C) | A.B+A.C | A+(B.C) | (A+B)(A+C) |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| Hukum Redudansi | ||||||
| A+A.B | A.(A+B) | A | 0+A | 0.A | 1+A | 1.A |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| A'+A | A'.A | A+A'B | A+B | A(A'+B) | A.B |
|
| 1 | 0 | 1 | 1 | 1 | 1 |
|
| 1 | 0 | 1 | 1 | 1 | 1 |
|
| 1 | 0 | 1 | 1 | 0 | 0 |
|
| 1 | 0 | 1 | 1 | 0 | 0 |
|
| 1 | 0 | 1 | 1 | 0 | 0 |
|
| 1 | 0 | 1 | 1 | 0 | 0 |
|
| 1 | 0 | 0 | 0 | 0 | 0 |
|
| 1 | 0 | 0 | 0 | 0 | 0 |
|
| Theoroma De Morgan’s | |||
| (A+B)' | A'.B' | (A.B)' | A'+B' |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |